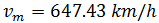Problemas de Movimiento Rectilíneo Uniforme

Problema 1

Un camión se mueve a velocidad constante de 90km/h por una autopista recta.

1. ¿qué distancia recorre en 2 horas?
2. ¿qué distancia recorre por segundo?
3. ¿cuánto tardará en recorrer 10km?
   
   Solución:
   
   La velocidad del camión es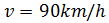
   
   expresada en kilómetros (espacio) por hora (tiempo).
   Apartado a:
   La ecuación del movimiento es
   
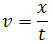   donde conocemos la velocidad y el tiempo. Queremos obtener la distancia recorrida: aislamos la x antes de sustituir en la ecuación:
   
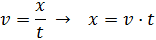   Ahora sustituimos los datos
   
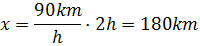   Hemos escrito las unidades de tiempo para tratarlas como factores, de este modo, como el tiempo, h, está multiplicando y dividiendo, desaparece, quedando únicamente la unidad de distancia, km.
   Por tanto, el camión recorre 180 kilómetros en 2 horas.
   Apartado b:
   De nuevo tenemos que calcular la distancia, pero ahora, en un tiempo de 1 segundo.
   Sabemos que la distancia recorrida es
   
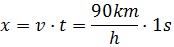   Notemos que en el denominador tenemos el tiempo en horas y en el numerador en segundos. Necesitamos la misma unidad. Para ello, pasaremos las horas a segundos.
   Una hora son
   
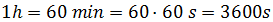   Entonces, escribimos 3600s donde tenemos la h:
   
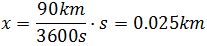   Como las unidades del tiempo son la misma, se han anulado.
   El espacio recorrido obtenido está en kilómetros, por lo que si queremos evitar los decimales podemos pasarlo a metros:
   
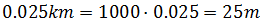   Por tanto, el camión recorre 25 metros cada segundo.
   Apartado c:
   Ahora sabemos la distancia, x = 10km , y tenemos que calcular el tiempo. Aislamos el tiempo en la ecuación:
   
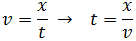   y sustituimos los datos
   
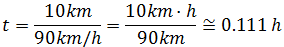   Notemos que las horas están dividiendo en el denominador, por lo que pasan multiplicando al numerador.
   Escribimos el tiempo en minutos para evitar los decimales:
   
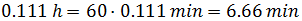   Para ser más exactos,
   
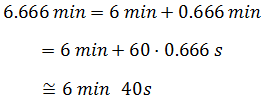   Por tanto, el camión tarda unos 6 minutos y 40 segundos en recorrer 10km.
   

   Problema 2

   La velocidad de la luz en el vacío es c = 300 000 km/s. La luz del Sol tarda en llegar a la Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.
   
   Solución:
   
   La velocidad la hemos llamado c en vez de v ya que para la luz se utiliza este nombre, pero el procedimiento es el mismo.
   Por tanto, conocemos la velocidad, c, y el tiempo, t = 8 min 19s. Podemos calcular la distancia: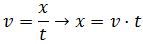
   
   Antes de sustituir tenemos que expresar el tiempo en una sola unidad. Como la velocidad la tenemos en kilómetros por segundo, pasamos el tiempo a segundos:
   Por un lado, los 8 minutos son
   
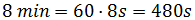   Por tanto, el tiempo es
   
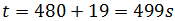   Ahora sustituimos los datos en la ecuación:
   
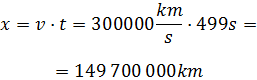   Por tanto, la distancia del Sol a la Tierra es de 149 700 000km, es decir, casi 150 millones de kilómetros.
   

   Problema 3

   En un movimiento rectilíneo con velocidad no constante, la velocidad media es
   
   
   donde x es la distancia recorrida final y t el tiempo transcurrido.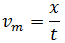
   La velocidad media es la velocidad que el móvil debería tener para recorrer la misma distancia en el mismo tiempo realizando un movimiento rectilíneo uniforme, es decir, con velocidad constante.
   Sabemos que un cohete espacial recorre 120km a una velocidad constante de 500km/h. Cuando alcanza los 120km, su velocidad pasa a ser, de forma instantánea, 900km/h. A esta velocidad recorre otros 120km.
   Calcular la velocidad media del cohete.
   
   Solución:
   
   
   En realidad, se trata de dos movimientos rectilíneos uniformes: uno durante los primeros 120 kilómetros y el otro durante los 120 kilómetros restantes.
   En cada uno de estos dos movimientos tenemos una velocidad distinta y, por tanto, como la distancia es la misma, cada movimiento tendrá una duración.
   En el primer movimiento, la velocidad es de 500km/h. Por tanto, tenemos la ecuación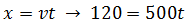
   
   El tiempo que dura el movimiento es de
   
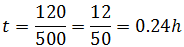   En el segundo, la velocidad es de 900km/h. Del mismo modo que antes, obtenemos que el tiempo es
   
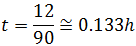   Por tanto, el tiempo total transcurrido es
   
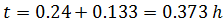   Y la distancia total recorrida es
   
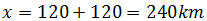   Ahora supongamos que realizamos un movimiento rectilíneo uniforme durante 0.373 horas y recorremos una distancia de 240 kilómetros. La velocidad de este movimiento es:
   
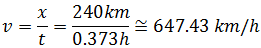   Por tanto, la velocidad media del cohete es
   

Magnitudes

En Física, se llaman magnitudes a aquellas propiedades que pueden medirse y expresar su resultado mediante un número y una unidad. Son magnitudes las longitud, la masa, el volumen, la cantidad de sustancia, el voltaje, etc. Las siguientes magnitudes se denominan magnitudes físicas fundamentales. Si a estas magnitudes se les añaden dos magnitudes complementarias: el ángulo sólido y el ángulo plano, a partir de ellas pueden expresarse TODAS las demás magnitudes físicas.

Magnitudes Símbolo Longitud x Masa m Tiempo t Temperatura T Intensidad de corriente eléctrica I,i Intensidad luminosa I Cantidad de sustancia mol

Potencia

En física, potencia (símbolo P) es la cantidad de trabajo efectuado por unidad de tiempo.

Si W es la cantidad de trabajo realizado durante un intervalo de tiempo de duración Δt, la potencia media durante ese intervalo está dada por la relación:

${\displaystyle {\bar {P}}\equiv \left\langle P\right\rangle ={\frac {\ W}{\Delta t}}}$

La potencia instantánea es el valor límite de la potencia media cuando el intervalo de tiempo Δt se aproxima a cero. En el caso de un cuerpo de pequeñas dimensiones:

${\displaystyle P(t)=\lim _{\Delta t\rightarrow 0}{\frac {\ W}{\Delta t}}\ =\lim _{\Delta t\rightarrow 0}\mathbf {F} \cdot {\frac {\Delta \mathbf {r} }{\Delta t}}=\mathbf {F} \cdot \mathbf {v} }$

Donde

P es la potencia,

W es el trabajo,

t es el tiempo.

r es el vector de posición.

F es la fuerza.

v es la velocidad.

Tipos de potencia

Potencia mecánica

La potencia mecánica aplicada sobre un sólido rígido viene dada por el producto de la fuerza resultante aplicada por la velocidad:

${\displaystyle P(t)=\mathbf {F} \cdot \mathbf {v} }$

Si además existe rotación del sólido y las fuerzas aplicadas están cambiando su velocidad angular:

${\displaystyle P(t)=\mathbf {F} \cdot \mathbf {v} +\mathbf {M} \cdot {\boldsymbol {\omega }}}$

donde:

${\displaystyle \mathbf {F} ,\mathbf {M} }$, son la fuerza resultante y el momento resultante.

${\displaystyle \mathbf {v} ,{\boldsymbol {\omega }}}$, son la velocidad del punto donde se ha calculado la resultante efectiva y la velocidad angular del sólido.

Para un sólido deformable o un medio continuo general la expresión es más compleja y se expresa como producto del tensor tensión y el campo de velocidades. La variación de energía cinética viene dada por:

${\displaystyle P={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V}{\frac {\rho }{2}}\|\mathbf {v} \|^{2}\ \mathrm {d} V+\int _{V}\sum _{ij}T_{ij}D_{ij}\ \mathrm {d} V}$

donde:

${\displaystyle T_{ij}}$, son las componentes del tensor de tensiones de Cauchy.

${\displaystyle D_{ij}}$, son las componentes del tensor de velocidad de deformación.

Potencia eléctrica

Artículo principal: Potencia eléctrica

La potencia eléctrica desarrollada en un cierto instante por un dispositivo viene dada por la expresión

${\displaystyle P(t)=I(t)V(t)\,}$

Donde:

P(t) es la potencia instantánea, medida en vatios (julios/segundo).

I(t) es la corriente que circula por él, medida en amperios.

V(t) es la diferencia de potencial (caída de voltaje) a través del componente, medida en voltios.

Si el componente es una resistencia, tenemos:

${\displaystyle P=I^{2}R={\frac {V^{2}}{R}}}$

Donde:

R es la resistencia, medida en ohmios.

Potencia calorífica

La potencia calorífica de un dispositivo es la cantidad de calor que libera por la unidad de tiempo:

${\displaystyle P={\frac {E}{t}}}$

P es la potencia instantánea, medida en vatios (julios/segundo).

E es la energía proporcionada en julios (J).

t es el tiempo en segundos (s).

Potencia sonora

La potencia sonora, considerada como la cantidad de energía que transporta la onda sonora por unidad de tiempo a través de una superficie dada, depende de la intensidad de la onda sonora y de la superficie , viniendo dada, en el caso general, por:

${\displaystyle P_{S}=\int _{S}I_{s}\ dS}$

• P_s es la potencia
• I_s es la intensidad sonora.
• dS es el elemento de superficie sobre alcanzado por la onda sonora.

Para una fuente aislada, el cálculo de la potencia sonora total emitida requiere que la integral anterior se extienda sobre una superficie cerrada.

Unidades de potencia

• Sistema Internacional (SI):
  • Vatio, (W):
• Sistema inglés:
  • caballo de fuerza o de potencia, horsepower en inglés, (hp)
    • 1 HP = 550 ft·lb_f/s
    • 1 HP = 745,7 W
• Sistema técnico de unidades:
  • kilográmetro por segundo, (kgm/s)
    • 1 kgm/s = 9,806215 W
  • kilocaloría por hora (kcal/h)
    • 1 kcal/h = 1000 cal/h = 1,1630556 W (vatio)
• Sistema cegesimal
  • ergio por segundo, (erg/s)
    • 1 erg/s = 1x10^-7 W
• Otras unidades:
  • caballo de vapor, (CV)
    • 1 CV = 75 kgf·m/s = 735,35375 W

Trabajo

Trabajo (W)
Trabajo realizado por una fuerza constante.
Magnitud	Trabajo (W)
Definición	Producto de la fuerza ejercida sobre un cuerpo por su desplazamiento
Tipo	Magnitud escalar
Unidad SI	Joule (J)
Otras unidades	Kilojoule (kJ) Kilográmetro (kgm)
[editar datos en Wikidata]

En mecánica clásica, se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo¹​ de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra ${\displaystyle \ W}$ (del inglés Work) y se expresa en unidades de energía, esto es en julios o joules (J) en el Sistema Internacional de Unidades.

Ya que por definición el trabajo es un tránsito de energía,²​ nunca se refiere a él como incremento de trabajo, ni se simboliza como ΔW.

Trabajo de una fuerza.

Consideremos una partícula ${\displaystyle P}$ sobre la que actúa una fuerza ${\displaystyle F}$, función de la posición de la partícula en el espacio, esto es ${\displaystyle F=F(\mathbf {r} )}$ y sea ${\displaystyle \mathrm {d} \mathbf {r} }$ un desplazamiento elemental (infinitesimal) experimentado por la partícula durante un intervalo de tiempo ${\displaystyle \mathrm {d} t}$. Llamamos trabajo elemental, ${\displaystyle \mathrm {d} W}$, de la fuerza ${\displaystyle \mathbf {F} }$ durante el desplazamiento elemental ${\displaystyle \mathrm {d} \mathbf {r} }$ al producto escalar ${\displaystyle \ F\cdot \mathrm {d} \mathbf {r} }$; esto es,

${\displaystyle \mathrm {d} W=\mathbf {F} \cdot \mathrm {d} \mathbf {r} \,}$

Si representamos por ${\displaystyle \mathrm {d} s}$ la longitud de arco (medido sobre la trayectoria de la partícula) en el desplazamiento elemental, esto es ${\displaystyle \mathrm {d} s=|\mathrm {d} \mathbf {r} |}$ , entonces el vector tangente a la trayectoria viene dado por ${\displaystyle \mathbf {e} _{\text{t}}=\mathrm {d} \mathbf {r} /\mathrm {d} s}$ y podemos escribir la expresión anterior en la forma

${\displaystyle \mathrm {d} W=\mathbf {F} \cdot \mathrm {d} \mathbf {r} =\mathbf {F} \cdot \mathbf {e} _{\text{t}}\mathrm {d} s=(F\cos \theta )\mathrm {d} s=F_{\text{s}}\mathrm {d} s\,}$

donde ${\displaystyle \theta }$ representa el ángulo determinado por los vectores ${\displaystyle \mathrm {d} \mathbf {F} }$ y ${\displaystyle \mathbf {e} _{\text{t}}}$ y ${\displaystyle F_{\text{s}}}$ es la componente de la fuerza F en la dirección del desplazamiento elemental ${\displaystyle \mathrm {d} \mathbf {r} }$.

El trabajo realizado por la fuerza ${\displaystyle \mathbf {F} }$ durante un desplazamiento elemental de la partícula sobre la que está aplicada es una magnitud escalar, que podrá ser positiva, nula o negativa, según que el ángulo ${\displaystyle \theta }$ sea agudo, recto u obtuso.

Si la partícula P recorre una cierta trayectoria en el espacio, su desplazamiento total entre dos posiciones A y B puede considerarse como el resultado de sumar infinitos desplazamientos elementales ${\displaystyle \mathrm {d} \mathbf {r} }$ y el trabajo total realizado por la fuerza ${\displaystyle \mathbf {F} }$ en ese desplazamiento será la suma de todos esos trabajos elementales; o sea

${\displaystyle W_{\text{AB}}=\int _{\text{A}}^{\text{B}}\mathbf {F} \cdot \mathrm {d} \mathbf {r} \,}$

Esto es, el trabajo viene dado por la integral curvilínea de ${\displaystyle \mathbf {F} }$ a lo largo de la curva ${\displaystyle C}$ que une los dos puntos; en otras palabras, por la circulación de ${\displaystyle \mathbf {F} }$ sobre la curva ${\displaystyle C}$ entre los puntos A y B. Así pues, el trabajo es una magnitud física escalar que dependerá en general de la trayectoria que una los puntos A y B, a no ser que la fuerza ${\displaystyle \mathbf {F} }$ sea conservativa, en cuyo caso el trabajo resultará ser independiente del camino seguido para ir del punto A al punto B, siendo nulo en una trayectoria cerrada. Así, podemos afirmar que el trabajo no es una variable de estado.