Problemas de Movimiento Rectilíneo Uniforme Acelerado

Problema 1
Describir el movimiento de la siguiente gráfica y calcular $v\left(0\right)$, $v\left(4\right)$, $v\left(10\right)$ y $v\left(15\right)$:

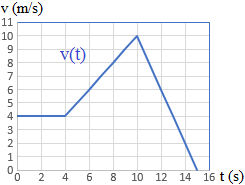
Es la gráfica de la velocidad en función del tiempo de un movimiento.

El movimiento es rectilíneo uniforme en el intervalo de tiempo [0,4], rectilíneo uniformemente acelerado con aceleración positiva en el intervalo [4,10] y rectilíneo uniformemente acelerado con aceleración negativa en el intervalo [10,15].

Observando la gráfica, las velocidades son

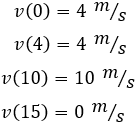
Problema 2

Calcular la aceleración (en $m/s^2$) que se aplica para que un móvil que se desplaza en línea recta a 90.0 km/h reduzca su velocidad a 50.0 km/h en 25 segundos.

Comentar el resultado.

La velocidad inicial del móvil es

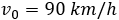
También conocemos la velocidad a los 25 segundos:

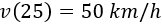
La fórmula de la velocidad es

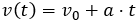
Despejamos la aceleración:

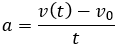
Antes de sustituir los datos, escribimos la velocidad en metros por segundo para tener las mismas unidades:

Sustituimos los datos en la fórmula de la aceleración que obtuvimos anteriormente:

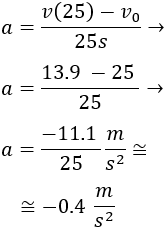
Por tanto, la aceleración es de $-0.4m/s^2$.

Como la velocidad inicial es positiva y el móvil va frenándose, entonces la aceleración es negativa.

Problema 3

Un tren de alta velocidad en reposo comienza su trayecto en línea recta con una aceleración constante de $a=0.5m/s^2$. Calcular la velocidad (en kilómetros por hora) que alcanza el tren a los 3 minutos.

Como el tren está en reposo, la velocidad inicial es 0:

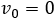
Nótese que la aceleración es en metros por segundos al cuadrado y el tiempo es en minutos. Debemos escribir el tiempo en segundos:

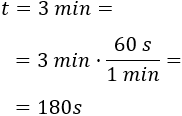
Calculamos la velocidad aplicando la fórmula:

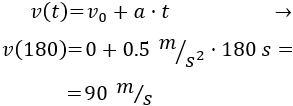
Tenemos la velocidad en metros por segundo, así que la escribimos en kilómetros por hora:

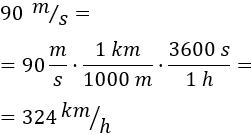
Por tanto, la velocidad del tren a los tres minutos es $324km/h$.