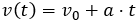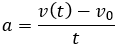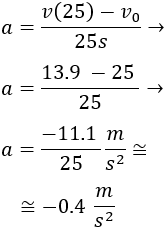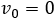Conversiones

La conversión de unidades es la transformación del valor numérico de una magnitud física, expresado en una cierta unidad de medida, en otro valor numérico equivalente y expresado en otra unidad de medida de la misma naturaleza.

Este proceso suele realizarse con el uso de los factores de conversión y/o las tablas de conversión de unidades.

Frecuentemente basta multiplicar por una fracción (factor de una conversión) y el resultado es otra medida equivalente, en la que han cambiado las unidades. Cuando el cambio de unidades implica la transformación de varias unidades, se pueden utilizar varios factores de conversión uno tras otro, de forma que el resultado final será la medida equivalente en las unidades que buscamos.

Por ejemplo, para pasar 8 metros a yardas, sabiendo que un metro equivale a 1,093613  , se multiplica 8 por 1,093613; lo que da por resultado 8,748904 yardas.

Problemas de tiro parabólico

Ejercicio 1

Un portero saca el balón desde el césped a una velocidad de 26 m/s. Si la pelota sale del suelo con un ángulo de 40° y cae sobre el campo sin que antes lo toque ningún jugador, calcular:

• Altura máxima del balón
• Distancia desde el portero hasta el punto donde caerá en el campo
• Tiempo en que la pelota estará en el aire

SOLUCIÓN:

Resolveremos el problema de dos maneras: aplicando directamente las fórmulas específicas o, en segundo lugar, partiendo de las ecuaciones de los dos movimientos, MRU y MRUA.

En primer lugar, descomponemos la velocidad inicial en sus componentes. La componente horizontal de la velocidad será:

La componente vertical de la velocidad inicial será:

La altura máxima será:

El alcance del saque del portero será:

Calcularemos el tiempo de vuelo de la pelota:

Ahora vamos a resolver el mismo problema, pero partiendo de las fórmulas de los dos movimientos componentes del movimiento parabólico: el movimiento rectilíneo uniforme (MRU), que se corresponde con el eje horizontal, y el movimiento rectilíneo uniformemente acelerado (MRUA), que se corresponde con el eje vertical. Recordemos que la aceleración aquí es la aceleración de la gravedad g, con valor -9,81 m/s² (signo negativo por ser el sentido de la gravedad contrario al de la componente vertical de la velocidad inicial v_0y).

En el punto en que el balón alcanza la altura máxima, su componente de velocidad vertical será vy = 0 m/s, ya que deja de subir y empieza a descender. Aplicamos la fórmula de la velocidad en el movimiento rectilíneo uniformemente acelerado (MRUA). En este caso será:

Como v_y = 0:

Tiempo que tarda en llegar el balón a su punto más alto. Ahora aplicamos la ecuación del espacio en el MRUA, para averiguar la altura máxima, sabiendo el tiempo que ha invertido en llegar a ella:

Nos queda saber el alcance. Como el movimiento parabólico es simétrico, tardará lo mismo en llegar al punto más alto que luego, desde allí, bajando llegar a tocar el césped, es decir 1,7 · 2 = 3,4 seg.

Aplicamos la fórmula del espacio del MRU, por más sencilla, que en este caso será:

Nota: la diferencia en los decimales en el resultado de los dos procedimientos se debe al redondeo.

Ejercicio 2

ANUNCIOS

Están jugando en el patio de un colegio, cuando el balón sale al exterior por encima de la valla del campo. Un hombre le da una patada al balón para devolverlo al interior. Sabiendo que el muro del patio tiene 3 m de altura, que el hombre está a 53 m del muro y que patea el balón a 24 m/s con un ángulo de 55°, averiguar si consigue que la pelota vuelva a entrar al patio pasando sobre el muro.

SOLUCIÓN:

En este problema, emplearemos también fórmulas de los dos movimientos componentes del movimiento parabólico: el movimiento rectilíneo uniforme (MRU), que se corresponde con el eje horizontal, y el movimiento rectilíneo uniformemente acelerado (MRUA), que se corresponde con el eje vertical.

En primer lugar, volvemos a descomponer el vector velocidad inicial v₀ en sus dos componentes. La componente horizontal de la velocidad será:

La componente vertical de la velocidad inicial será:

Resolveremos el problema aplicando las ecuaciones de los dos movimientos, MRU y MRUA. Como el hombre chuta el balón a 53 m del muro y la componente horizontal de la velocidad es 13,77 m/s, por la ecuación del MRU tendremos:

Que será el tiempo en llegar al balón al muro, ya que éste está a 53 m. Ahora, para ver si lo sobrepasa, aplicamos una fórmula del MRUA:

Recordamos que la aceleración es la de la gravedad g, con signo contrario al de la componente vertical de la velocidad inicial.

La respuesta al ejercicio es que el hombre no ha conseguido meter el balón en el patio, puesto que el muro tiene una altura de 3 m y el balón ha impactado contra él a 2,98 m. Deberá volverlo a intentar, quizás acercándose más al muro.

Ejercicio 3

En una prueba de atletismo de lanzamiento de peso, el atleta logra una marca de 22 m. Sabiendo que la bola sale de su mano a 2 m del suelo y con un ángulo de 45°, averiguar la velocidad inicial del lanzamiento.

SOLUCIÓN:

Para resolver el problema, igualmente emplearemos las fórmulas del movimiento rectilíneo uniforme y del movimiento rectilíneo uniformemente acelerado, que componen,como se ha repetido, el movimiento parabólico. Del movimiento MRU usaremos la fórmula:

Sabemos que v₀ · cos θ es la componente horizontal de la velocidad v₀). Despejamos el tiempo y la velocidad:

Ahora, vamos a la fórmula del espacio del movimiento rectilíneo uniformemente acelerado:

Sabemos también que v₀ · sen θ es la componente vertical de la velocidad v₀ y que la aceleración es la de la gravedad g con signo negativo, al ser contraria a la velocidad inicial. La altura final será cero, y = 0 m, puesto que la bola impacta en el suelo. La altura inicial será a la que suelta el atleta la bola de la mano, y₀ = 2 m). Sustituimos por la expresión de t antes obtenida y ponemos los valores conocidos:

Despejamos de esta ecuación la t, pues tan 45° = 1.

Volvemos a la expresión anterior de v₀.

Por lo tanto, 14,1 m/s será la velocidad de lanzamiento v₀ buscada.

Problemas de caída libre

Ejercicio 1. Un cuerpo cae libremente desde el reposo durante 6 segundos hasta llegar al suelo. Calcular la distancia que ha recorrido, o lo que es lo mismo, la altura desde donde se soltó. 

 Datos que tenemos:

 Velocidad inicial ………. Vo = 0 (la soltamos y parte de velocidad cero)
 Tiempo de caída …….…... t = 6 s 
 Aceleración de caída …... g = 10 m/s2 (aproximamos en lugar de 9,8)
 Altura final será el suelo = 0 (Nota: aunque no fuera el suelo en caída libre la altura final siempre = 0)
 Parte de una altura inicial Yo = ??? es la que nos piden, también podemos llamarla altura o "h".
Solución: Y = vo t + Yo - 0.5 gt² donde Yo será la altura inicial o altura desde la que cae (h).

 poniendo valores en la fórmula : 

 0 = Yo -0.5 ( 10 x 6²)  ==> despejando Yo

 -Yo = - 180  Los signos menos se nos marchan en los dos miembros de la ecuación y quedarán positivos.

 Yo = 180m Resuelto  h = 180 metros

 Ejercicio 2. Un tornillo cae accidentalmente desde la parte superior de un edificio. 4 segundos después está golpeando el suelo. ¿Cual será la altura del edificio?. 

 Datos iniciales: 

 Velocidad inicial ................... Vo = 0 
 tiempo de caída ...................... t = 4s 
 aceleración de caída ............... g = 10 m/s2 
 altura de caída (edificio ) .......... h = ?  (en la fórmula será Yo)

Solución:  Y = vo t + Yo - 0.5 gt² o lo que es lo mismo Y = Vo . t - 1/2 gt². En nuestro caso tenemos qué:

 0 = Yo - 1/2 ( 10 x 4²) = => 0 = Yo - 80 ;despejando Yo

 Yo = 80 metros Resuelto
 Ejercicio 3. Desde el techo de un edificio se deja caer una piedra hacia abajo y se oye el ruido del impacto contra el suelo 3 segundos después. Sin tomar en cuenta la resistencia del aire, ni el tiempo que tardó el sonido en llegar al oído, calcula:

 a) La altura del edificio.
 b) La velocidad de la piedra al llegar al suelo.

  Considerar g = 10 m/s²

Solución: Primero calculamos el apartado b). Aplicamos la primera fórmula: V = Vo +- gt, para calcular la velocidad a la que llega al suelo, sabiendo que Vo = cero y que el signo es + por ir cada vez más rápido la piedra. La fórmula quedará V = gt

 V = 10 x 3 = 30 m/s Resuelto.

 Ahora para el apartado a) aplicamos la segundo fórmula sabiendo que Y (final) es cero por que acaba en el suelo y la Vo sigue siendo cero también. La fórmula quedará:

 Y = Yo - 0.5 gt²

 0 = Yo - (0.5 x 10 x 3²) = Yo - 35 Despejando Yo tenemos:

 Yo = 45 metros Resuelto.

Problemas de tiro vertical

Problema n° 1) Se lanza un cuerpo verticalmente hacia abajo con una velocidad inicial de 7 m/s.

a) ¿Cuál será su velocidad luego de haber descendido 3 s?

b) ¿Qué distancia habrá descendido en esos 3 s?

c) ¿Cuál será su velocidad después de haber descendido 14 m?

d) Si el cuerpo se lanzó desde una altura de 200 m, ¿en cuánto tiempo alcanzará el suelo?

e) ¿Con qué velocidad lo hará?

Usar g = 10 m/s².

Solución:

a) De la ecuación (1):

vf = (7 m/s) + (10 m/s²).(3 s)
vf = 37 m/s

b) De la ecuación (2):

Δh = (7 m/s).(3 s) + (10 m/s²).(3 s)²/2
Δ h = 66 m

c) De la ecuación (3):

vf = √v0² + 2.g.h

vf = 18,14 m/s

d) De la ecuación (2):

0 = v0.t + g.t²/2 - y

Aplicamos la ecuación cuadrática que dará dos resultados:

t1 = 5,66 s

t2 = -7,06 s (NO ES SOLUCION)

e) De la ecuación (3):

vf = √v0² + 2.g.h

vf = 63,63 m/s

Problema n° 2) Se lanza un cuerpo verticalmente hacia arriba con una velocidad inicial de 100 m/s, luego de 4 s de efectuado el lanzamiento su velocidad es de 60 m/s.

a) ¿Cuál es la altura máxima alcanzada?

b) ¿En qué tiempo recorre el móvil esa distancia?

c) ¿Cuánto tarda en volver al punto de partida desde que se lo lanzo?

d) ¿Cuánto tarda en alcanzar alturas de 300 m y 600 m?

Usar g = 10 m/s².

Solución:

a) Para la altura máxima vf = 0, de la ecuación (3):

-v0² = 2.g.h
h máx = -vf²/(2.g)⇒ h máx = -(100 m/s)²/[2.(-10 m/s²)]

h máx = 500 m

b) De la ecuación (1) y para vf = 0:

t = v0/g

t = (-100 m/s)/(-10 m/s²)

t = 10 s

c) Recordemos que en tiro vertical, cuando un objeto es lanzado hacia arriba y luego cae, cuando vuelve a pasar por el punto de partida posee la misma velocidad que en el momento del lanzamiento pero con sentido contrario (vf = -v0).

Podemos asegurar que el resultado pedido es el doble del tiempo que requirió para alcanzar la altura máxima.

t = 20 s

e) No puede alcanzar una altura de 600 m porque la máxima es de 500 m. Para h = 300 m empleamos la ecuación (2):

0 = v0.t + g.t²/2 - y

Aplicamos la ecuación cuadrática (Báscara) que dará dos resultados:

t1 = 3,67 s

t2 = 16,32 s

Problema n° 3) Un observador situado a 40 m de altura ve pasar un cuerpo hacia arriba con una cierta velocidad y al cabo de 10 s lo ve pasar hacia abajo, con una velocidad igual en módulo pero de distinto sentido.

a) ¿Cuál fue la velocidad inicial del móvil?

b) ¿Cuál fue la altura máxima alcanzada?

Usar g = 10 m/s².

Solución:

a) Los 10 s se componen de 5 s hasta alcanzar la altura máxima (vf = 0) y 5 s para regresar, de la ecuación (1):

0 = v0 + g.t
v0 = -g.t
v0 = -(-10 m/s²).(5 s)
v0 = 50 m/s (a nivel del observador).

Esta velocidad inicial la tomaremos como la final usando la fórmula (3):

vf² - v0² = 2.g.h

(50 m/s)² - v0² = 2.(-10 m/s²).(40 m)

(50 m/s)² - 2.(-10 m/s²).(40 m) = v0²

v0 = 57,45 m/s (a nivel de lanzamiento)

b) Nuevamente con la ecuación (3) calculamos la distancia recorrida desde el observador hasta la altura final:

vf² - v0² = 2.g.h

(0 m/s)² - (50 m/s)² = 2.(-10 m/s²).h

h = 125 m

Finalmente sumamos la altura máxima y la altura del observador:

h = 125 m + 40 m

h = 165 m

Problemas de Movimiento Rectilíneo Uniforme Acelerado

Problema 1
Describir el movimiento de la siguiente gráfica y calcular $v\left(0\right)$, $v\left(4\right)$, $v\left(10\right)$ y $v\left(15\right)$:

Es la gráfica de la velocidad en función del tiempo de un movimiento.

El movimiento es rectilíneo uniforme en el intervalo de tiempo [0,4], rectilíneo uniformemente acelerado con aceleración positiva en el intervalo [4,10] y rectilíneo uniformemente acelerado con aceleración negativa en el intervalo [10,15].

Observando la gráfica, las velocidades son

Problema 2

Calcular la aceleración (en $m/s^2$) que se aplica para que un móvil que se desplaza en línea recta a 90.0 km/h reduzca su velocidad a 50.0 km/h en 25 segundos.

Comentar el resultado.

La velocidad inicial del móvil es

También conocemos la velocidad a los 25 segundos:

La fórmula de la velocidad es

Despejamos la aceleración:

Antes de sustituir los datos, escribimos la velocidad en metros por segundo para tener las mismas unidades:

Sustituimos los datos en la fórmula de la aceleración que obtuvimos anteriormente:

Por tanto, la aceleración es de $-0.4m/s^2$.

Como la velocidad inicial es positiva y el móvil va frenándose, entonces la aceleración es negativa.

Problema 3

Un tren de alta velocidad en reposo comienza su trayecto en línea recta con una aceleración constante de $a=0.5m/s^2$. Calcular la velocidad (en kilómetros por hora) que alcanza el tren a los 3 minutos.

Como el tren está en reposo, la velocidad inicial es 0:

Nótese que la aceleración es en metros por segundos al cuadrado y el tiempo es en minutos. Debemos escribir el tiempo en segundos:

Calculamos la velocidad aplicando la fórmula:

Tenemos la velocidad en metros por segundo, así que la escribimos en kilómetros por hora:

Por tanto, la velocidad del tren a los tres minutos es $324km/h$.